Convolution
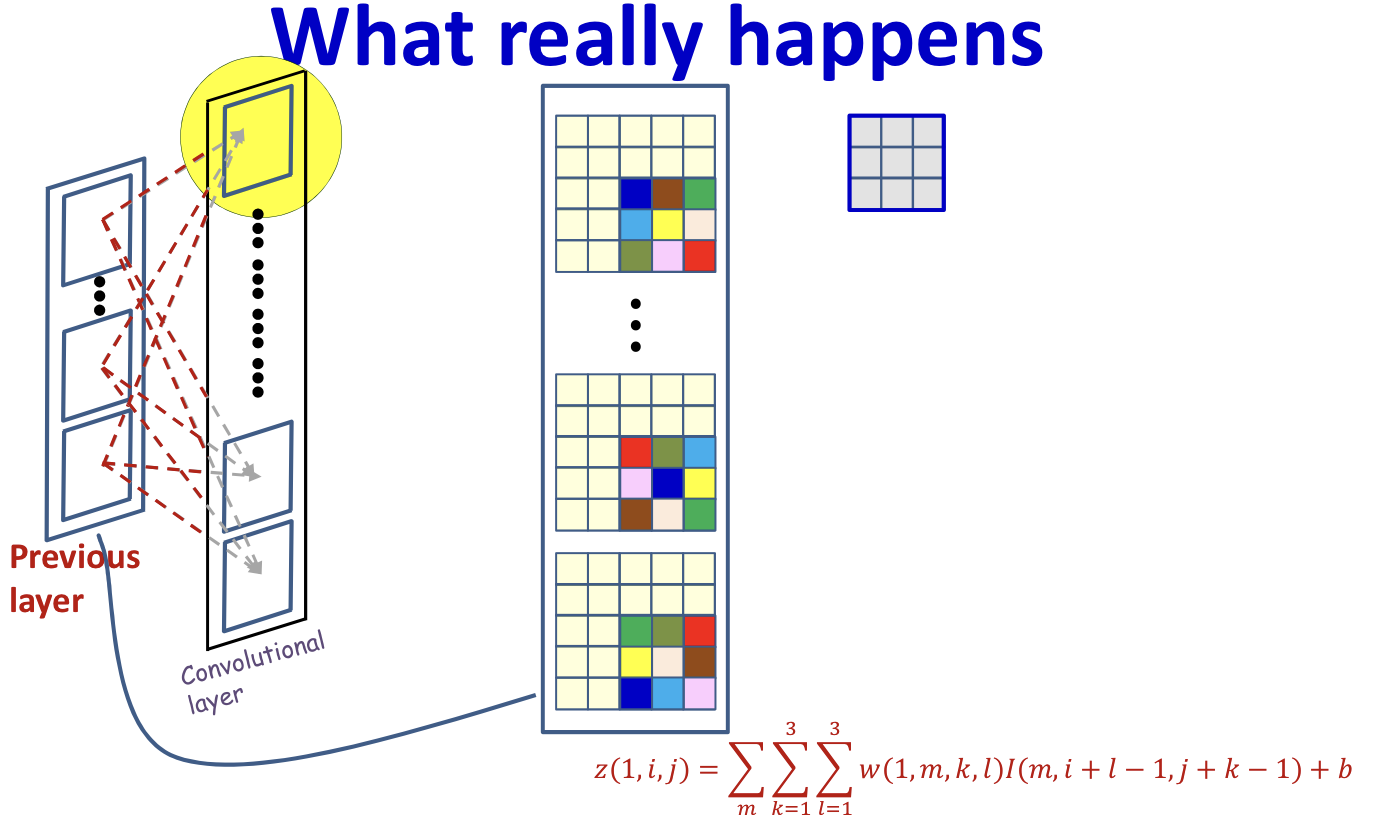
- Each position in consists of convolution result in previous map

- Way for shrinking the maps
- Stride greater than 1
- Downsampling (not necessary)
- Typically performed with strides > 1
- Pooling
- Maxpooling
- Note: keep tracking of location of max (needed while back prop)
- Mean pooling
- Maxpooling
Learning the CNN
- Training is as in the case of the regular MLP
- The only difference is in the structure of the network
- Define a divergence between the desired output and true output of the network in response to any input
- Network parameters are trained through variants of gradient descent
- Gradients are computed through backpropagation

Final flat layers
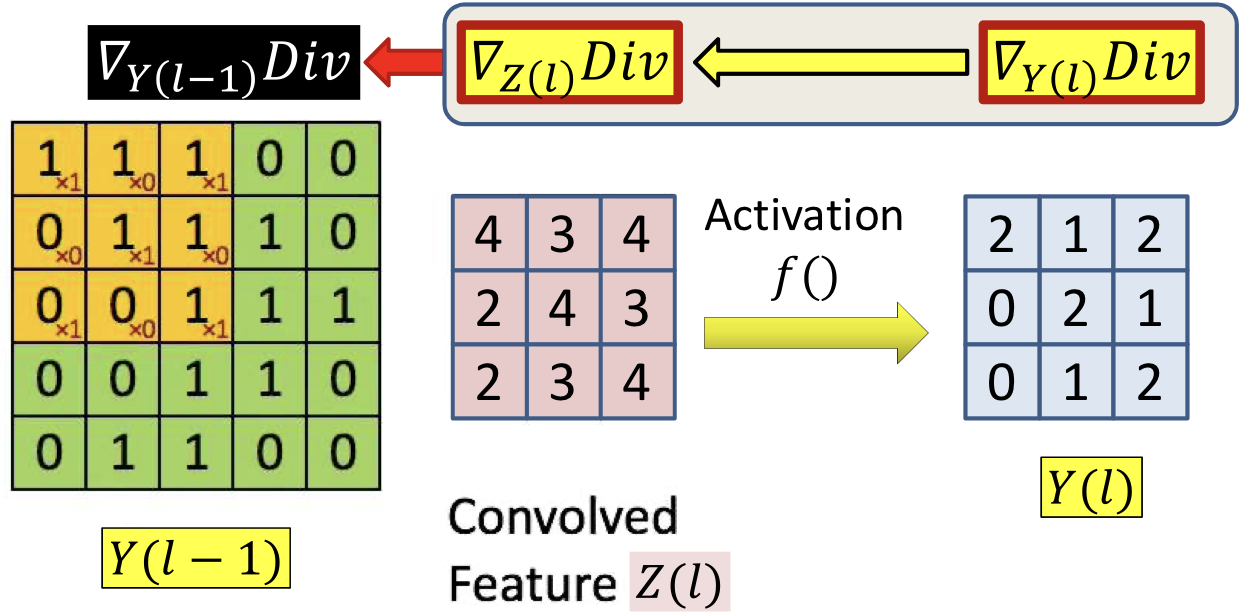
- Backpropagation continues in the usual manner until the computation of the derivative of the divergence
- Recall in Backpropagation
- Step 1: compute 、
- Step 2: compute according to step 1
Convolutional layer
Computing
Simple compont-wise computation
Computing
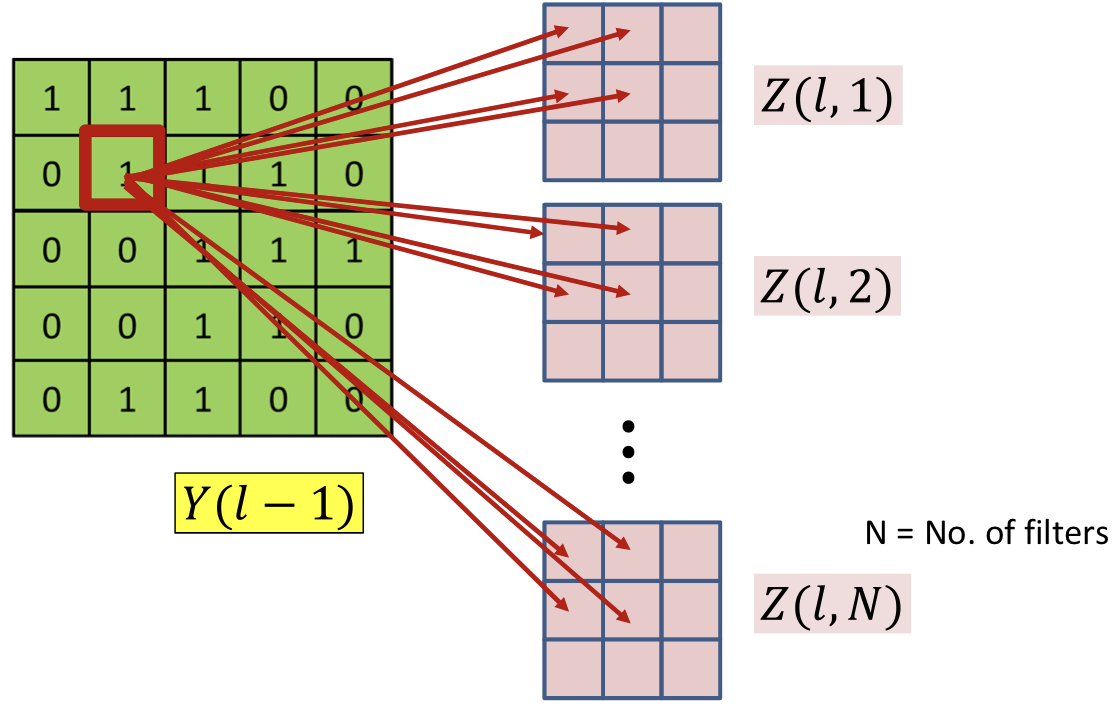
Each affects several terms for every (map)
- Through
- Affects terms in all layer maps
- All of them contribute to the derivative of the divergence
Derivative w.r.t a specific term
Computing
- Each weight also affects several term for every
- Affects terms in only one map (the nth map)
- All entries in the map contribute to the derivative of the divergence w.r.t.
- Derivative w.r.t a specific term
Summary

In practice
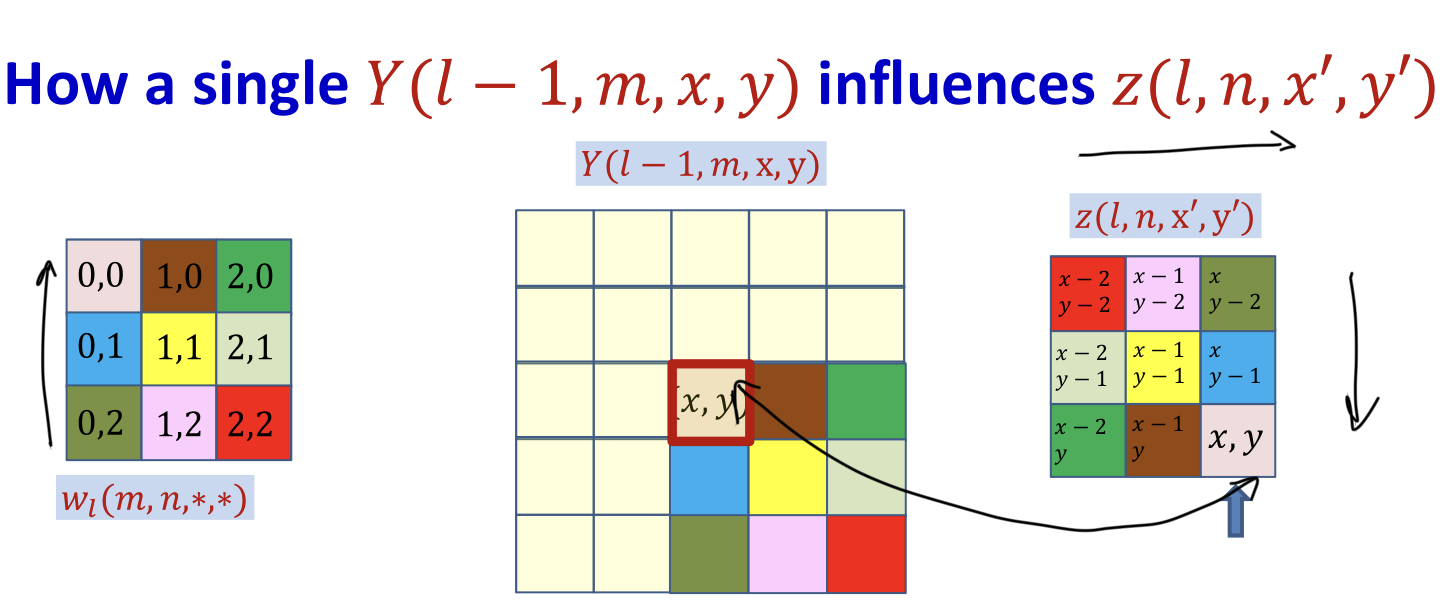
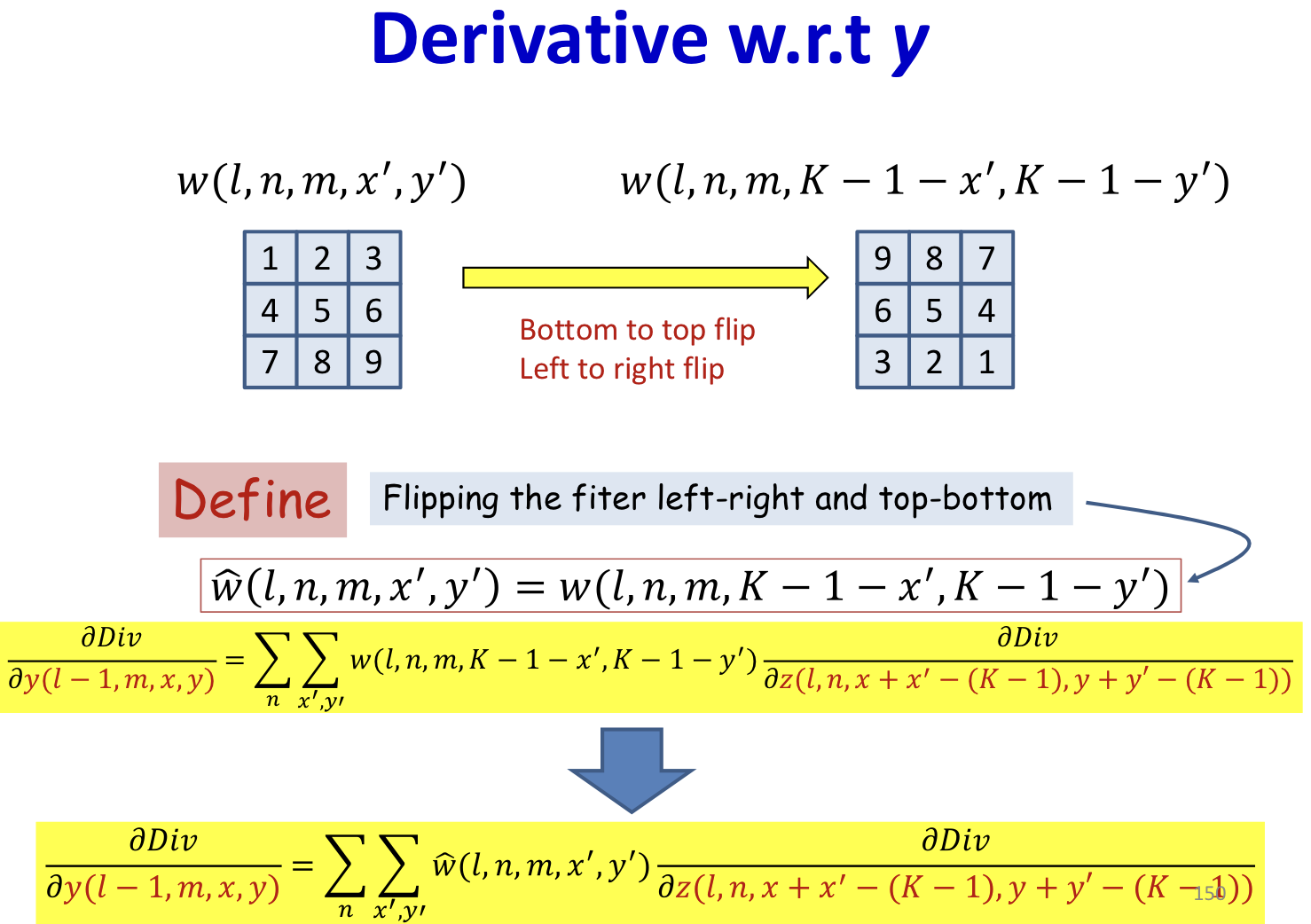
- This is a convolution, with defferent order
- Use mirror image to do normal convolution (flip up down / flip left right)
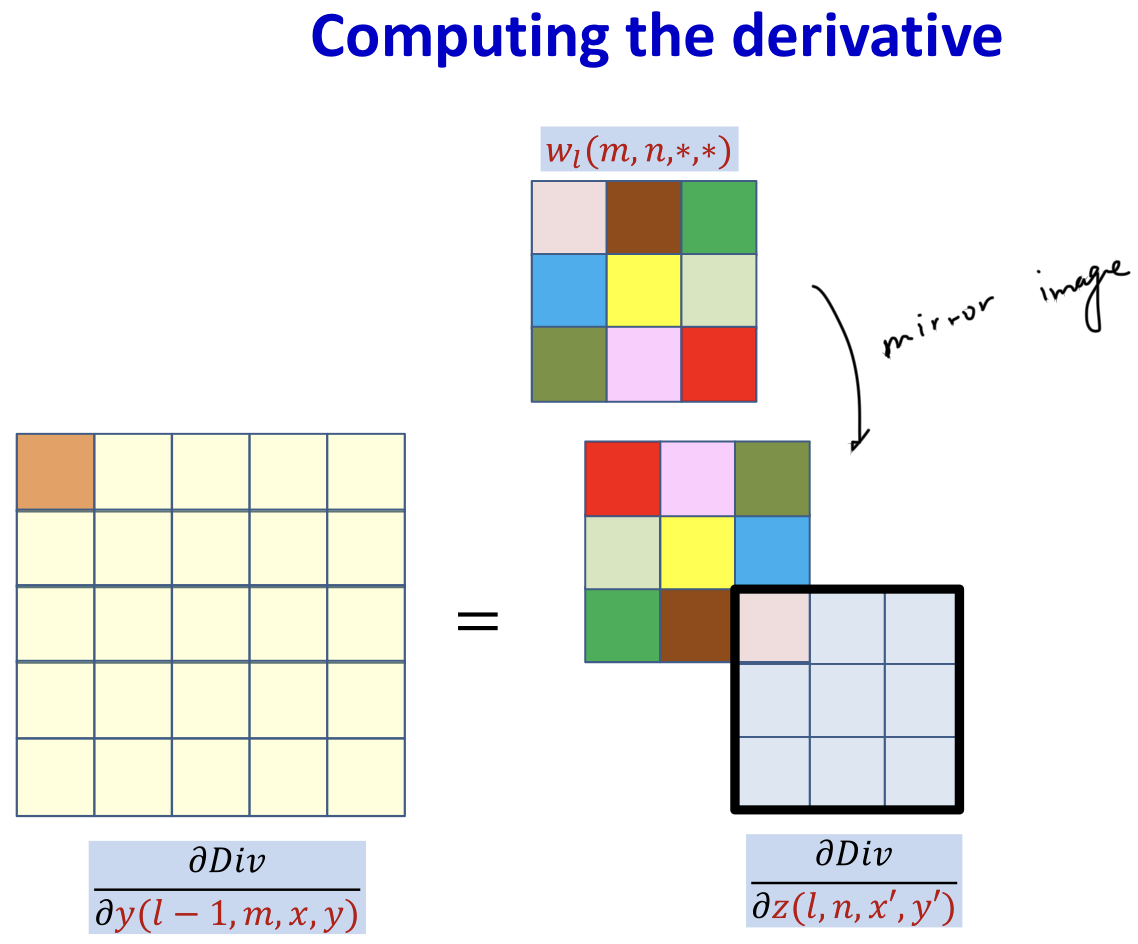
- In practice, the derivative at each (x,y) location is obtained from all maps
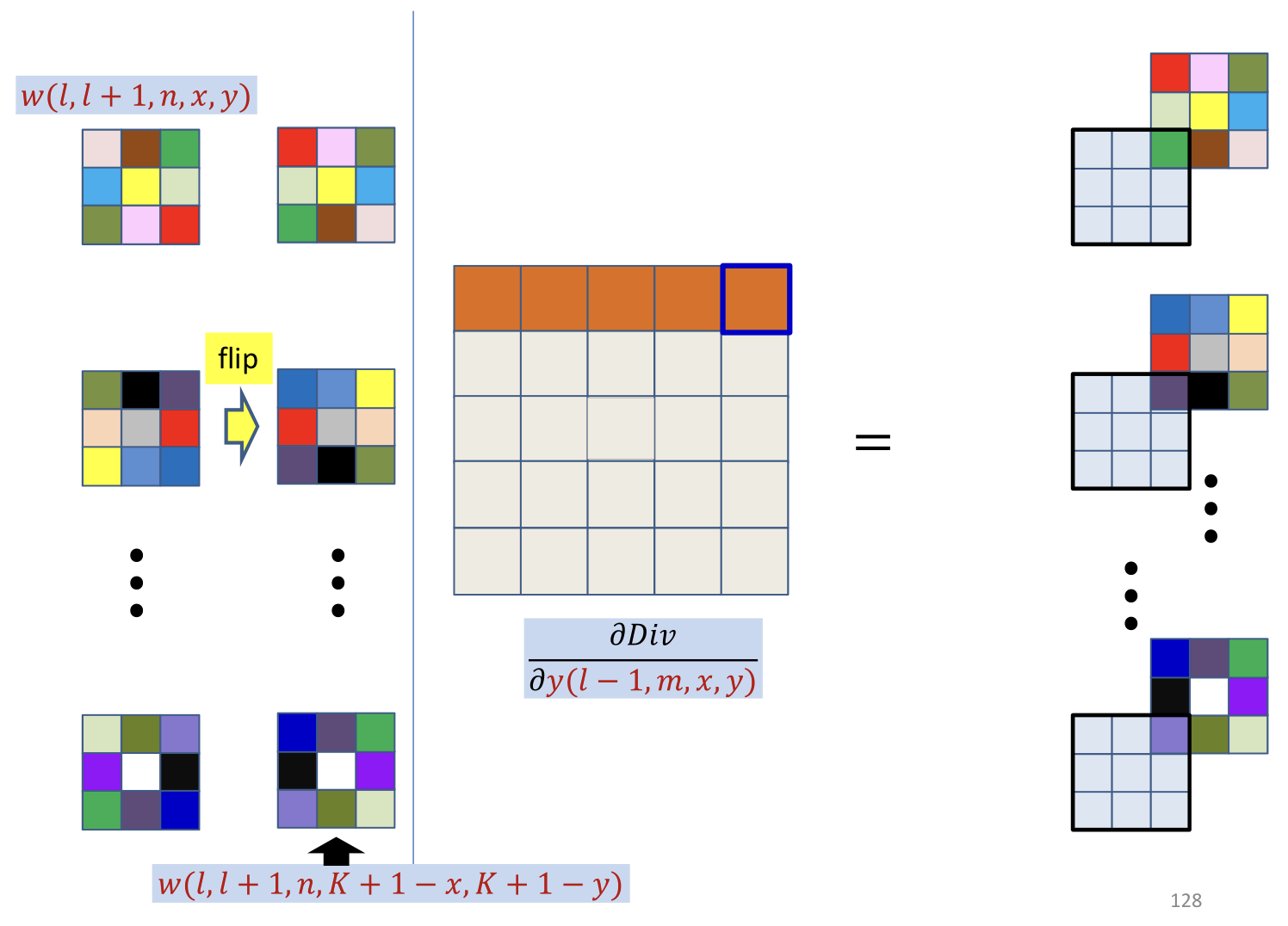
- This is just a convolution of by the inverted filter
- After zero padding it first with zeros on every side
- Note: the refer to the location in filter
- Shifting down and right by , such that becomes
- Regular convolution running on shifted derivative maps using flipped filter
Pooling
- Pooling is typically performed with strides > 1
- Results in shrinking of the map
- Downsampling
Derivative of Max pooling
- Max pooling selects the largest from a pool of elements 1

Derivative of Mean pooling
- The derivative of mean pooling is distributed over the pool

Transposed Convolution
- We’ve always assumed that subsequent steps shrink the size of the maps
- Can subsequent maps increase in size 2
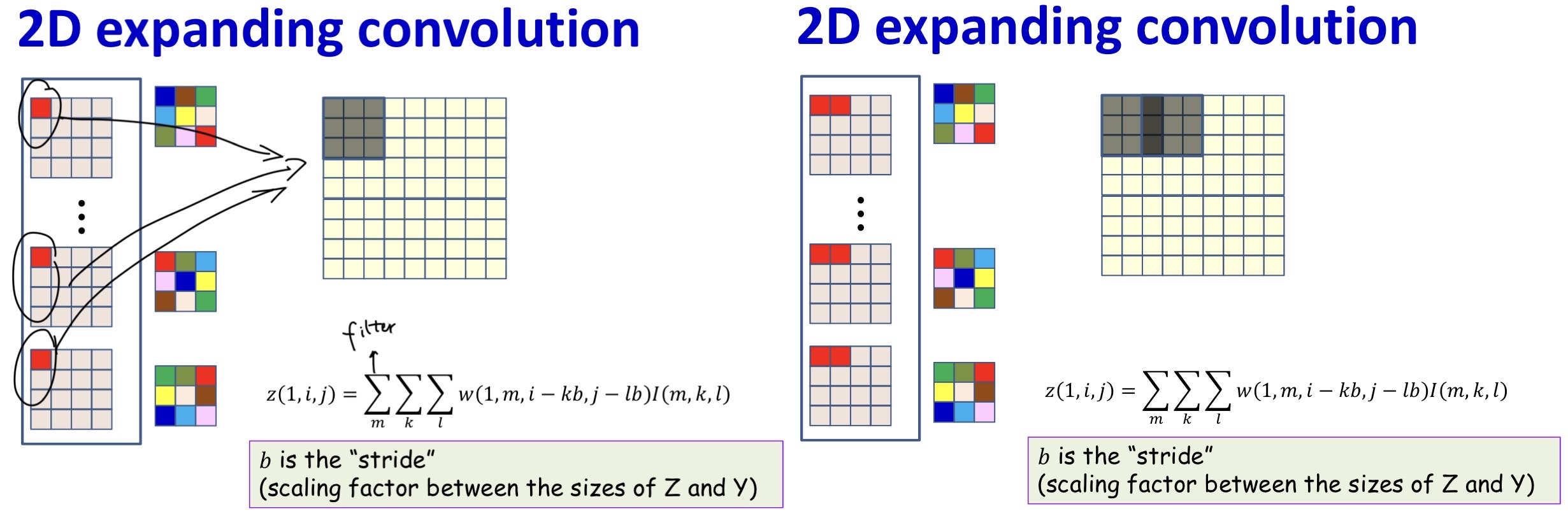
- Output size is typically an integer multiple of input
- +1 if filter width is odd
Model variations
- Very deep networks
- 100 or more layers in MLP
- Formalism called “Resnet”
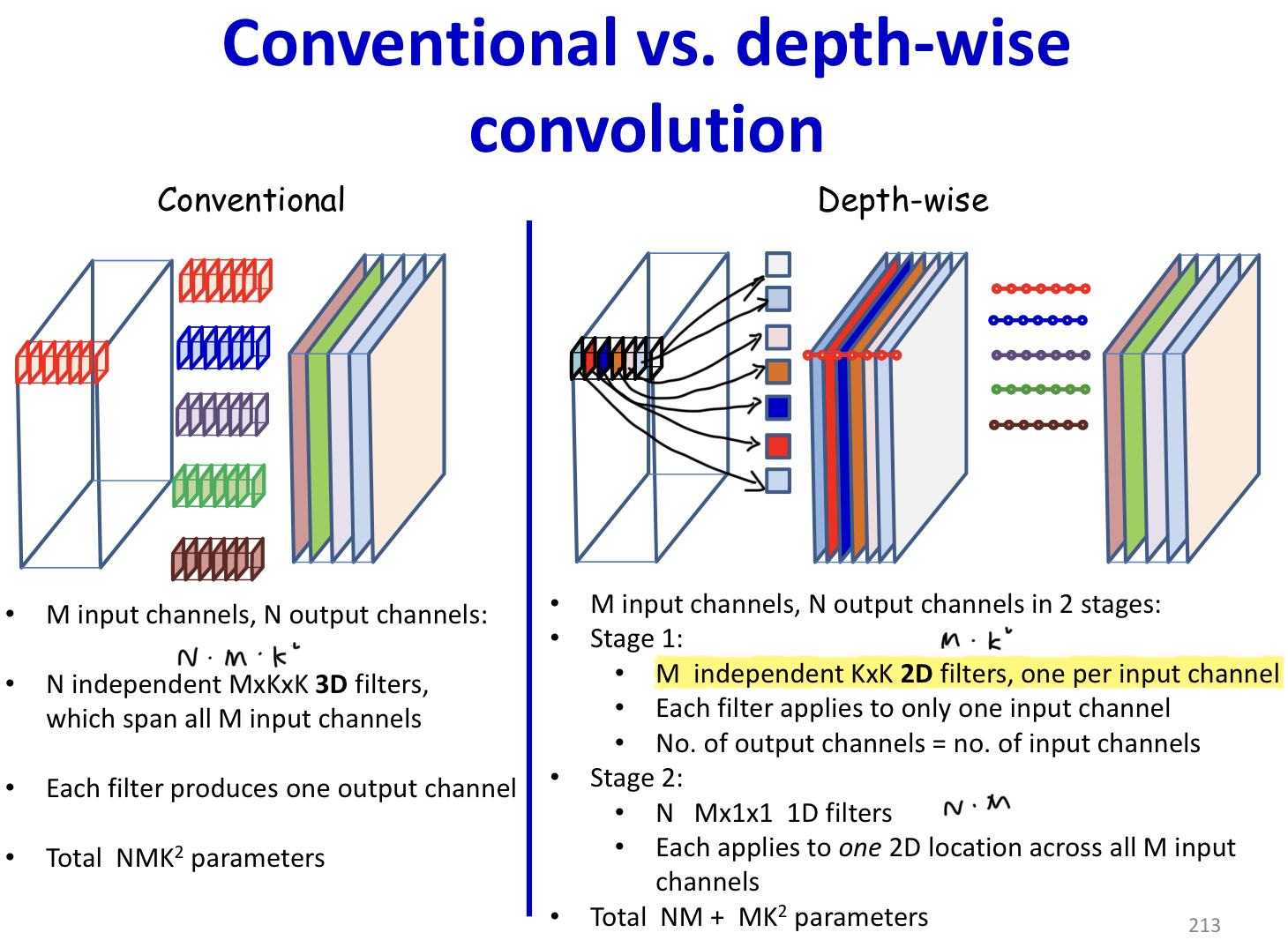
- Depth-wise convolutions
- Instead of multiple independent filters with independent parameters, use common layer-wise weights and combine the layers differently for each filter
Depth-wise convolutions
- In depth-wise convolution the convolution step is performed only once
- The simple summation is replaced by a weighted sum across channels
- Different weights (for summation) produce different output channels
Models
For CIFAR 10
- Le-net 5 3
For ILSVRC(Imagenet Large Scale Visual Recognition Challenge)
- AlexNet
- NN contains 60 million parameters and 650,000 neurons
- 5 convolutional layers, some of which are followed by max-pooling layers
- 3 fully-connected layers
- VGGNet
- Only used 3x3 filters, stride 1, pad 1
- Only used 2x2 pooling filters, stride 2
- ~140 million parameters in all
- Googlenet
- Multiple filter sizes simultaneously
- AlexNet
For ImageNet
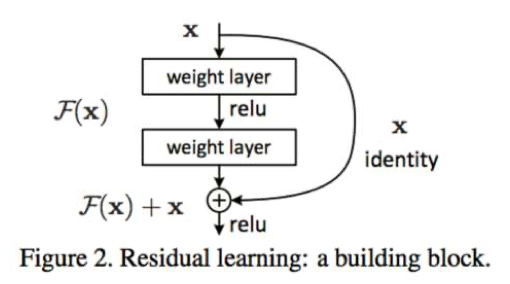
- Resnet
- Last layer before addition must have the same number of filters as the input to the module
- Batch normalization after each convolution
- Densenet
- All convolutional
- Each layer looks at the union of maps from all previous layers
- Instead of just the set of maps from the immediately previous layer
- Resnet
1. Backprop Through Max-Pooling Layers? ↩
2. Transposed Convolution Demystified ↩
3. https://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html ↩